7.5 符号表及其基本实现
本文首先介绍了什么是符号表,以及这一抽象数据结构的的API,然后介绍了两种简单的符号表的实现方式。
一符号表
在开始介绍查找算法之前,我们需要定义一个名为符号表(Symbol Table)的抽象数据结构,该数据结构类似我们再C#中使用的Dictionary,他是对具有键值对元素的一种抽象,每一个元素都有一个key和value,我们可以往里面添加key,value键值对,也可以根据key来查找value。在现实的生活中,我们经常会遇到各种需要根据key来查找value的情况,比如DNS根据域名查找IP地址,图书馆根据索引号查找图书等等:
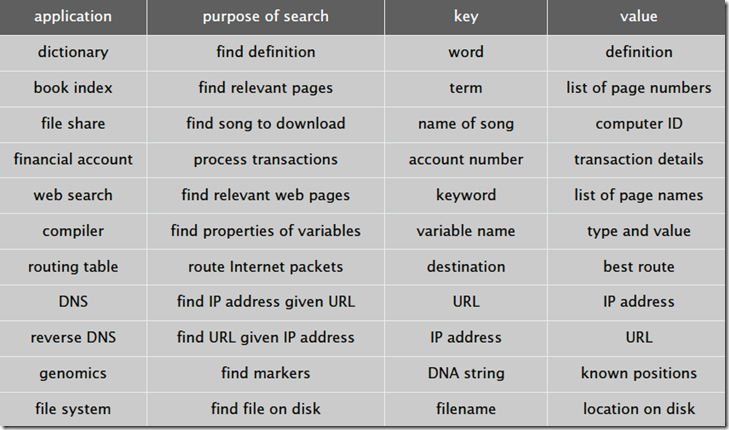
为了实现这一功能,我们定义一个抽象数据结构,然后选用合适的数据结构来实现:
public class ST
| ST() | 创建一个查找表对象 |
|---|---|
| void Put(Key key, Value val) | 往集合中插入一条键值对记录,如果value为空,不添加 |
| Value Get(Key key) | 根据key查找value,如果没找到返回null |
| void Delete(Key key) | 删除键为key的记录 |
| boolean Contains(Key key) | 判断集合中是否存在键为key的记录 |
| boolean IsEmpty() | 判断查找表是否为空 |
| int Size() | 返回集合中键值对的个数 |
| Iterable |
返回集合中所有的键 |
二实现
1 使用无序链表实现查找表
查找表的实现关键在于数据结构的选择,最简单的一种实现是使用无序链表来实现,每一个节点记录key值,value值以及指向下一个记录的对象。
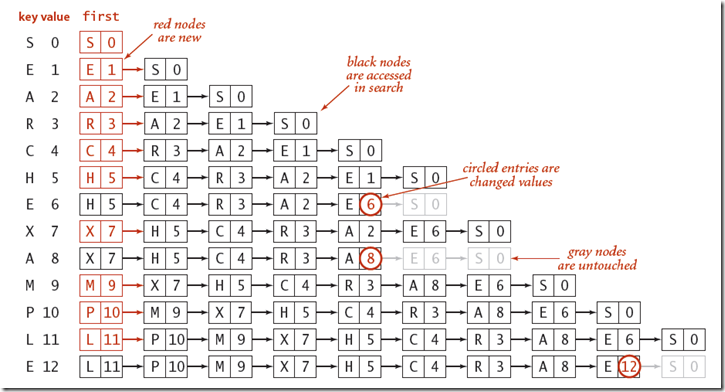
如图,当我们往链表中插入元素的时候,从表头开始查找,如果找到,则更新value,否则,在表头插入新的节点元素。
实现起来也很简单:
public class SequentSearchSymbolTable<TKey, TValue> : SymbolTables<TKey, TValue> where TKey : IComparable<TKey>, IEquatable<TKey>
{
private int length = 0;
Node first;
private class Node
{
public TKey key { get; set; }
public TValue value { get; set; }
public Node next { get; set; }
public Node(TKey key, TValue value, Node next)
{
this.key = key;
this.value = value;
this.next = next;
}
}
public override TValue Get(TKey key)
{
TValue result = default(TValue);
Node temp = first;
while (temp != null)
{
if (temp.key.Equals(key))
{
result = temp.value;
break;
}
temp = temp.next;
}
return result;
}
public override void Put(TKey key, TValue value)
{
Node temp = first;
while (temp != null)
{
if (temp.key.Equals(key))
{
temp.value = value;
return;
}
temp = temp.next;
}
first = new Node(key, value, first);
length++;
}
....
}
分析:
从图或者代码中分析可知,插入的时候先要查找,如果存在则更新value,查找的时候需要从链表头进行查找,所以插入和查找的平均时间复杂度均为O(n)。那么有没有效率更好的方法呢,下面就介绍二分查找。
2 使用二分查找实现查找表
和采用无序链表实现不同,二分查找的思想是在内部维护一个按照key排好序的二维数组,每一次查找的时候,跟中间元素进行比较,如果该元素小,则继续左半部分递归查找,否则继续右半部分递归查找。整个实现代码如下:
class BinarySearchSymbolTable<TKey, TValue> : SymbolTables<TKey, TValue> where TKey : IComparable<TKey>, IEquatable<TKey>
{
private TKey[] keys;
private TValue[] values;
private int length;
private static readonly int INIT_CAPACITY = 2;
public BinarySearchSymbolTable(int capacity)
{
keys = new TKey[capacity];
values = new TValue[capacity];
length = capacity;
}
public BinarySearchSymbolTable() : this(INIT_CAPACITY)
{
}
/// <summary>
/// 根据key查找value。
/// 首先查找key在keys中所处的位置,如果在length范围内,且存在该位置的值等于key,则返回值
/// 否则,不存在
/// </summary>
/// <param name="key"></param>
/// <returns></returns>
public override TValue Get(TKey key)
{
int i = Rank(key);
if (i < length && keys[i].Equals(key))
return values[i];
else
return default(TValue);
}
/// <summary>
/// 向符号表中插入key,value键值对。
/// 如果存在相等的key,则直接更新value,否则将该key,value插入到合适的位置
/// 1.首先将该位置往后的元素都往后移以为
/// 2.然后再讲该元素放到为i的位置上
/// </summary>
/// <param name="key"></param>
/// <param name="value"></param>
public override void Put(TKey key, TValue value)
{
int i = Rank(key);
if (i < length && keys[i].Equals(key))
{
values[i] = value;
return;
}
//如果长度相等,则扩容
if (length == keys.Length) Resize(2 * keys.Length);
for (int j = length; j > i; j--)
{
keys[j] = keys[j - 1];
values[j] = values[j - 1];
}
keys[i] = key;
values[i] = value;
length++;
}
/// <summary>
/// 返回key在数组中的位置
/// </summary>
/// <param name="key"></param>
/// <returns></returns>
private int Rank(TKey key)
{
int lo = 0;
int hi = length - 1;
while (lo <= hi)
{
int mid = lo + (hi - lo) / 2;
if (key.CompareTo(keys[mid]) > 0) lo = mid + 1;
else if (key.CompareTo(keys[mid]) < 0) hi = mid - 1;
else return mid;
}
return lo;
}
。。。
}
这里面重点是Rank方法,我们可以看到首先获取mid位置,然后将当前元素和mid位置元素比较,然后更新lo或者hi的位置用mid来替换,如果找到相等的,则直接返回mid,否则返回该元素在集合中应该插入的合适位置。上面是使用迭代的方式来实现的,也可以改写为递归:
private int Rank(TKey key, int lo, int hi)
{
if (lo >= hi) return lo;
int mid = lo + (hi - lo) / 2;
if (key.CompareTo(keys[mid]) > 0)
return Rank(key, mid + 1, hi);
else if (key.CompareTo(keys[mid]) < 0)
return Rank(key, lo, hi - 1);
else
return mid;
}
二分查找的示意图如下:
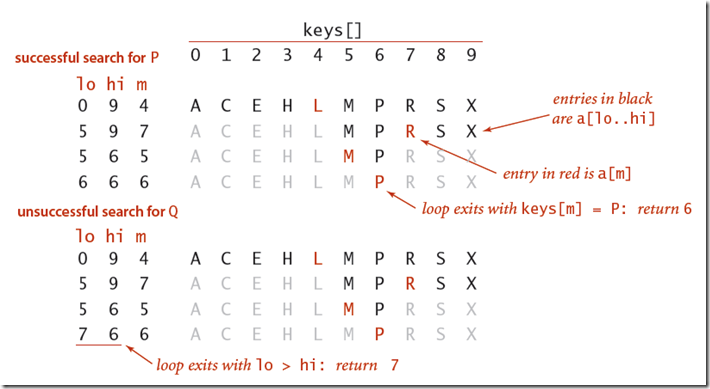
分析:
使用有序的二维数组来实现查找表可以看出,采用二分查找只需要最多lgN+1次的比较即可找到对应元素,所以查找效率比较高。
但是对于插入元素来说,每一次插入不存在的元素,需要将该元素放到指定的位置,然后,将他后面的元素依次后移,所以平均时间复杂度O(n),对于插入来说效率仍然比较低。
三 总结
本文介绍了符号表这一抽象数据结构,然后介绍了两种基本实现:基于无序链表的实现和基于有序数组的实现,两种实现的时间复杂度如下:
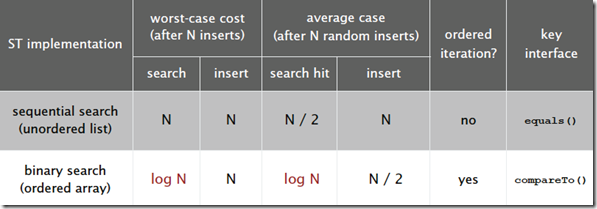
可以看到,使用有序数组的二分查找法提高了符号表的查找速度,但是插入效率仍旧没有得到提高,而且在要维护数组有序,还需要进行排序操作。这两种实现方式简单直观,但是无法同时达到较高查找和插入效率。那么有没有一种数据结构既能够在查找的时候有较高的效率,在插入的时候也有较好的效率呢,本文只是一个引子,后面的系列文章将会介绍二叉查找树,平衡查找树以及哈希表。